Trig identities tan^2 219761-Trig identities tan^2

 · Meanwhile trigonometric identities are equations that involve trigonometric functions that are always true This identities mostly refer to one angle labelled $ \displaystyle \theta $ {\tan }}^{3}}\theta }}{{13{{{\tan }}^{2}}\theta }}$ Half Angle Identities The first and second identities take minus or plus sign depending on the quadrant270 ° Show AnswerSin 2 (x) cos 2 (x) = 1 tan 2 (x) 1 = sec 2 (x) cot 2 (x) 1 = csc 2 (x) sin(x y) = sin x cos y cos x sin y cos(x y) = cos x cosy sin x sin y

Tangent Half Angle Formula Wikipedia

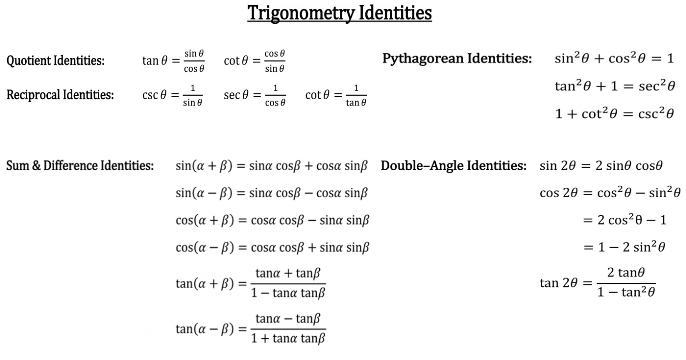
Trig identities tan^2

Trig identities tan^2-Trigonometric Identities Pythagoras's theorem sin2 cos2 = 1 (1) 1 cot2 = cosec2 (2) tan2 1 = sec2 (3) Note that (2) = (1)=sin 2 and (3) = (1)=cos CompoundThe half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 Verify the identity Example 6 Verify the identity tan (α/2) = (1 − cos α)/sin α Example 7 Verify the identity tan (α − 2) = sin π/(1 cos α)

Example 1 Verify A Trigonometric Identity The Left Hand Side Of This Identity Is More Complicated So Transform That Expression Into The One On The Right Ppt Download

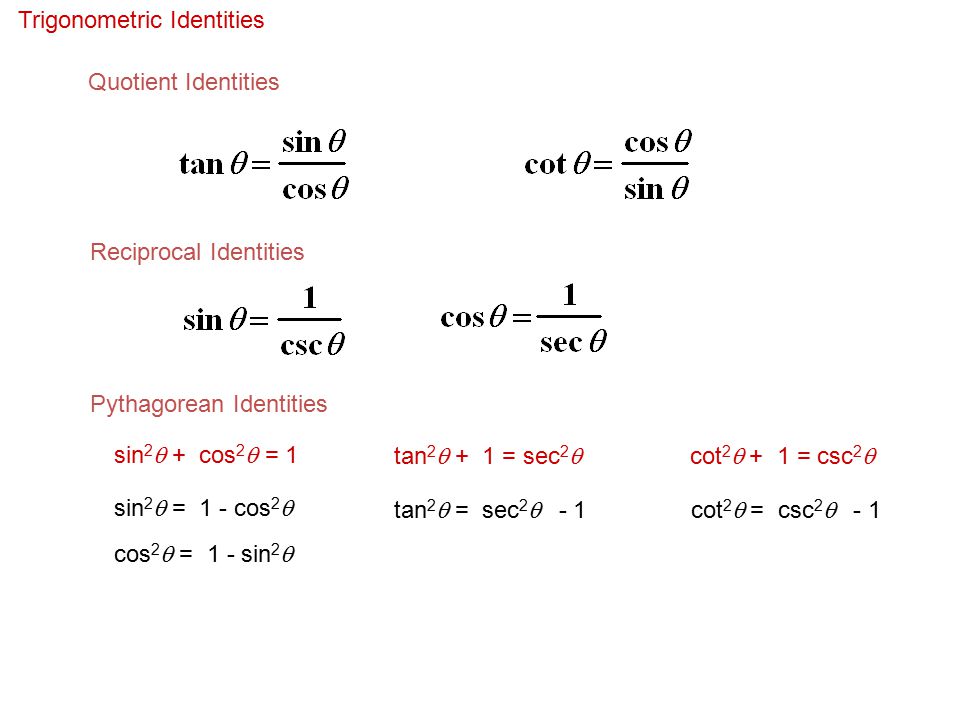
Free trigonometric identity calculator verify trigonometric identities stepbystep This website uses cookies to ensure you get the best experience ByPythagorean Trig Identities Pythagoras Trig Identities are the trigonometric identities which actually the true representation of the Pythagoras Theorem as trigonometric functions So, these identities help us to fundamentally decide the relationship between different sine, cosine, and tan trigonometric function1 tan 2 θ = sec 2 θ and cot 2 θ 1 = cosec 2 θ (Try dividing the second expression by cos 2 θ to get the first rearrangement, and separately divide cos 2 θ sin 2 θ = 1, by sin 2 θ to get the other formula) These are Trigonometric Identities and useful for rewriting equations so that they can be solved, integrated, simplified etc

 · Simplify tan^2 x sec^2 Ans 1 Use trig identity 1 tan^2 x = sec^2 x tan^2 x sec^2 x = 1Using the fundemental identities and the Pythagorean Identities, I go over multiple examples of verifying trigonometric identities It is very important in pLHS = 1 sin ⁡ θ cos ⁡ θ = ( 1 sin ⁡ θ) cos ⁡ θ) × ( 1 − sin ⁡ θ) 1 − sin ⁡ θ = 1 − sin 2 ⁡ θ cos ⁡ θ ( 1 − sin ⁡ θ) = cos 2 ⁡ θ cos ⁡ θ ( 1 − sin ⁡ θ) = cos ⁡ θ ( 1 − sin ⁡ θ) = RHS Restrictions undefined where cos ⁡ θ = 0, sin ⁡ θ = 1 and where tan ⁡ θ is undefined Therefore θ ≠ 90 °;

Sums or difference of Sines or Cosines · tan²θ = sin²θ cos²θ = 1 That is wrong tan²θ = sin²θ/cos²θ Secondly, the identity is tan²θ 1 = sec²θ, not tan²θ 1 Maybe this proof will be easier to followGraphs of Inverse Trigonometric Functions;

List Of Trigonometric Identities Wikiwand

Revision Trigonometry Siyavula

Trig ratios for an acute angle θ;By dividing the identity sin2 θcos2 θ ≡ 1 by (a) sin2 θ (b) cos2 θ obtain two further identities Hint Recall the definitions of cosecθ, secθ, cotθ Your solution Answer (a) sin 2θ sin2 θ cos2 θ sin 2θ = 1 sin θ (b) sin θ cos 2θ cos2 θ cos θ = 1 cos2 θ 1 cot2θ ≡ cosec2θ tan2 θ 1 ≡ sec2θ Key Point 13 introduces two further important identitiesTan is an "odd" identity quotient identity (for tangent) algebra/ simplify 1) 2) cos tan (x) Strategy 1) get rid of the negatives 2) üy to change terms to sin's and COS's 3) simplFy • tan (x) tan x sm x cos x smx cos (x) cosx • cosx • Prove Strategy

Solved 1 Using Various Trig Identities Determine The Ex Chegg Com

Derivatives Of Trigonometric Functions

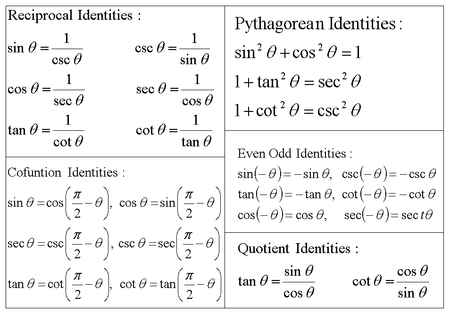
Trig identities or a trig substitution mcTYintusingtrig091 Some integrals involving trigonometric functions can be evaluated by using the trigonometric identities These allow the integrand to be written in an alternative form which may be more amenable to integrationIdentities expressing trig functions in terms of their complements cos t = sin(/2 – t) sin t = cos(/2 – t) cot t = tan(/2 – t) tan t = cot(/2 – t) csc t = sec(/2 – t) sec t = csc(/2 – t) Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2D is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4

Trigonometric Identities Solutions Examples Videos

Tangent Half Angle Formula Wikipedia

Answer to Verify the following trig identity 1/(cot^2 x) 1/(tan^2 x) = sec^2 x csc^2 x By signing up, you'll get thousands of stepbystepList of identities Given two functions f and g, we say f = g if f(x) = g(x) for all every x in the domain of both f and gThe key Pythagorean Trigonometric identity are sin 2 (t) cos 2 (t) = 1 tan 2 (t) 1 = sec 2 (t) 1 cot 2 (t) = csc 2 (t) So, from this recipe, we can infer the equations for different capacities additionally Learn more about Pythagoras Trig Identities Dividing through by c 2 gives a 2/ c 2 b 2/ c 2 = c 2/ c 2 This can be simplified to (a/c) 2 (b/c) 2 = 1

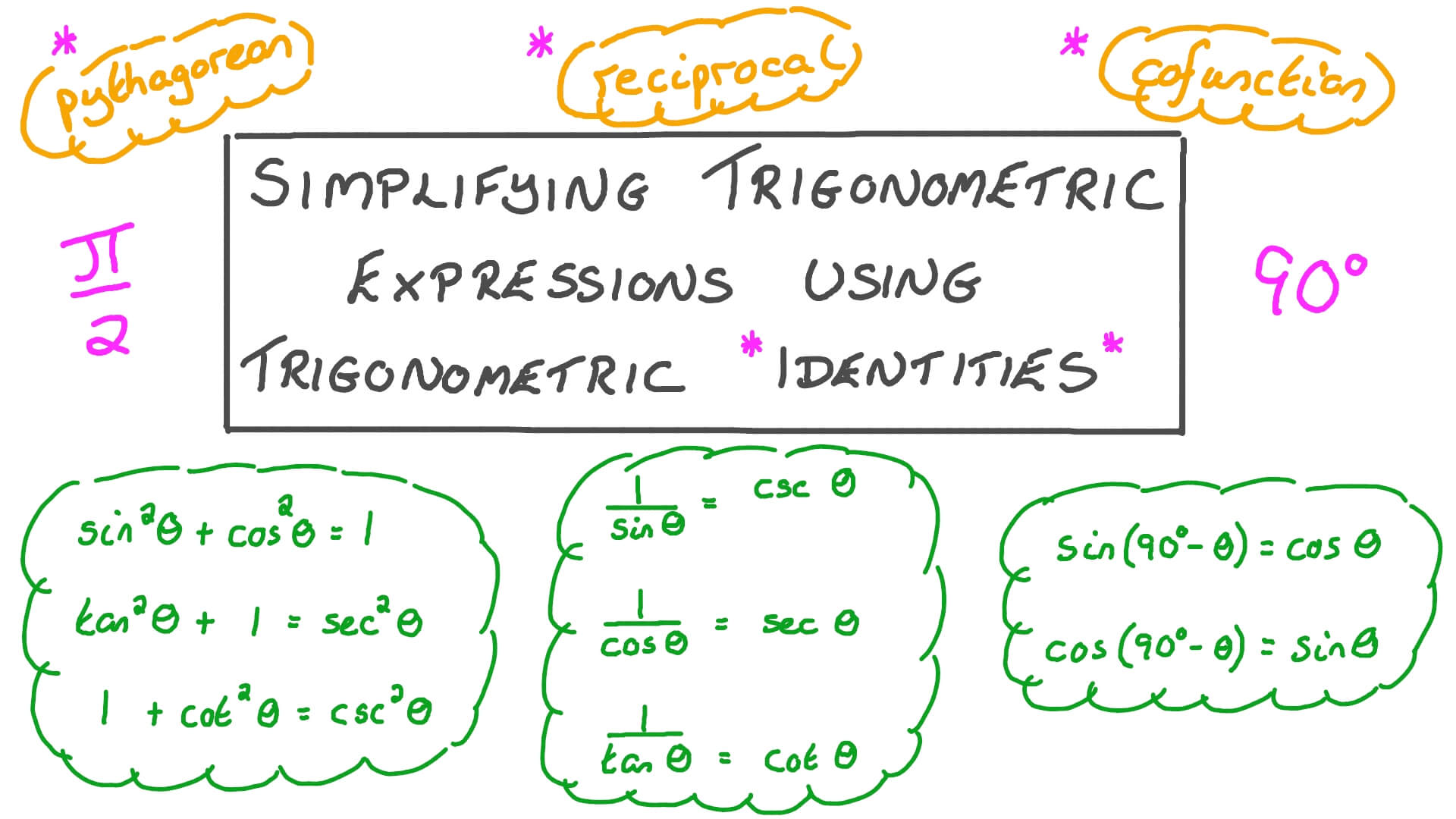
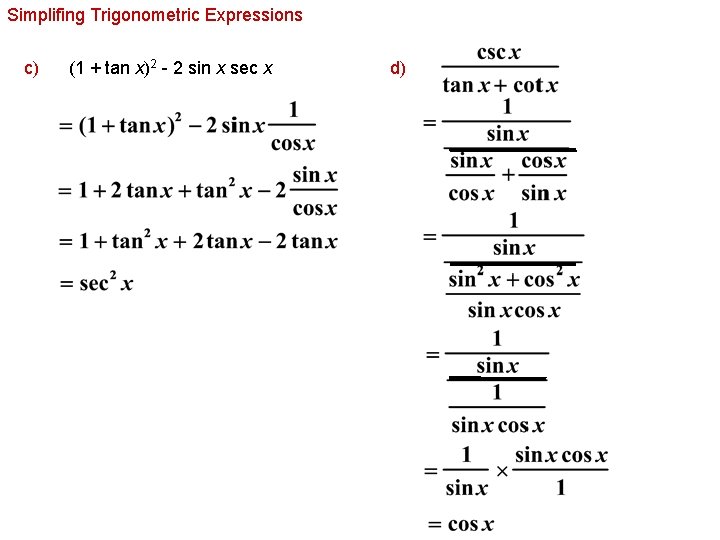
Lesson Video Simplifying Trigonometric Expressions Using Trigonometric Identities Nagwa

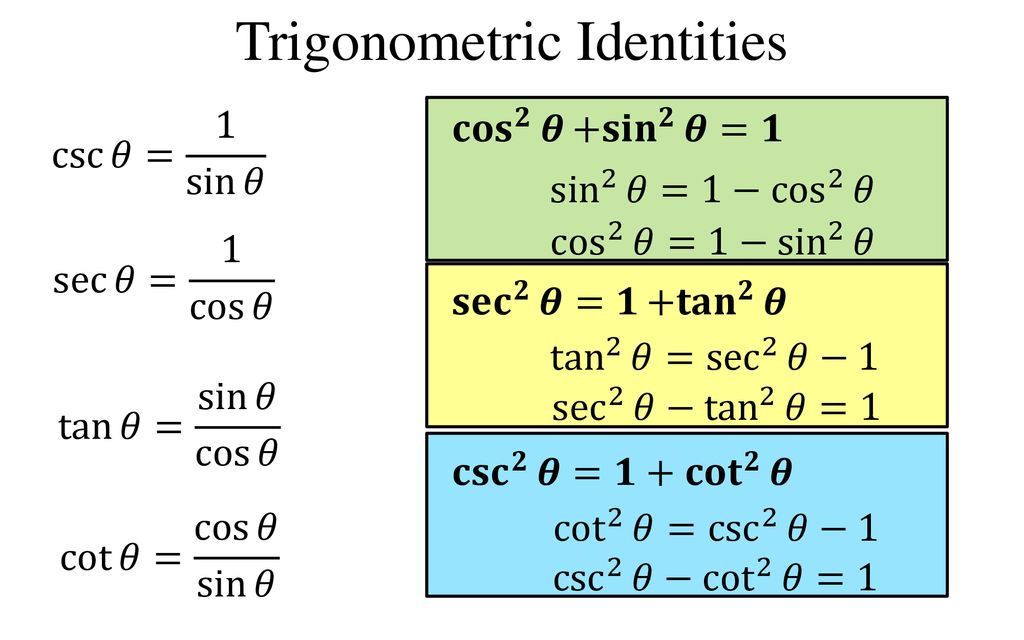
Trigonometric Identities And Equations Ppt Download

Trigonometric Identities From Math Wiki Jump to navigation Jump to search Contents 1 List of identities;The six trigonometric functions are defined for every real number, except, for some of them, for angles that differ from 0 by a multiple of the right angle (90°)Referring to the diagram at the right, the six trigonometric functions of θ are, for angles smaller than the right angleFree math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantly

Summary Of Trigonometric Identities

How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube

 · Using the following tan(x) = sin(x)/cos(x) cos^2(x)sin^2(x) = 1 sec(x) = 1/cos(x) for cos(x)!=0, we have 1tan^2(x) = cos^2(x)/cos^2(x) (sin(x)/cos(x))^2 =cos^2(xStudents are taught about trig identities or trigonometric identities in school and are an important part of higherlevel mathematics So to help you understand and learn all trig identities we have explained here all the concepts of trigonometryAs a student, you would find the trig identity sheet we have provided here useful So you can download and print the identities PDFThey are as follows (sinx)′ = cosx, (cosx)′ = −sinx Using the quotient rule it is easy to obtain an expression for the derivative of tangent (tanx)′ = ( sinx cosx)′ = (sinx)′ cosx−sinx(cosx)′ cos2x = cosx⋅ cosx−sinx⋅ (−sinx) cos2x = cos2xsin2x cos2x = 1 cos2x

Example 1 Verify A Trigonometric Identity The Left Hand Side Of This Identity Is More Complicated So Transform That Expression Into The One On The Right Ppt Download

How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic

Trigonometric Integrals In this section we use trigonometric identities to integrate certain combinations of trigonometric functions We start with powers of sine and cosine y tan6x 1 tan2x sec 2x dx y tan6x sec4x dx y tan6x sec2x sec2x dx u tan xNow, using the trigonometric identity 1tan 2 a = sec 2 a sec 2 A = 1 (3/4) 2 sec 2 A = 25/16 sec A = ±5/4 Since, the ratio of lengths is positive, we can neglect sec A = 5/4 Therefore, sec A = 5/4 Example 2 (1 – sin A)/(1 sin A) = (sec A – tan A) 2 Solution Let us take the Left hand side of the equation LHS = (1 – sin A)/(1 sin A)Trig functions of Angles outside the range 0° to 90° Here are diagrams of an angle in each of the four quadrants of a circle, snapshots from the excellent How the Trigonometry Functions Are Related from the Wolfram Demonstrations Project by C Ormullion Click in a quadrant to see a typical angle and all 6 trig functions

Summary Of Trigonometric Identities

14 2 Trigonometric Identities

All the trigonometric identities on one page Color coded Mobile friendly With PDF and JPG downloads Trig Identities Download PDF Download JPG Reciprocal Identities I highly recommend this 3minute $$ \tan(2\theta) = \frac{2\tan\theta}{1\tan^2\theta} $$All three of the trigonometric functions of an angle are related If we know the value of one of the three, we can calculate the other two (up to sign) by using the Pythagorean and tangent identities Prove the identity \(~~1 \tan^2 t = \dfrac{1}{\cos^2 t}\) SolutionBe familiar with trigonometric functions that can be integrated easily Be familiar with common identities – especially squared terms sin 2 x , cos 2 x , tan 2 x , cosec 2 x , sec 2 x , tan 2 x all appear in identities

Solved Trig Identities 1 Sin Cos 2 Sin Cos 2 2 2 Tan2 Cos2 Cot2 Sin2 1 3 Sec Course Hero

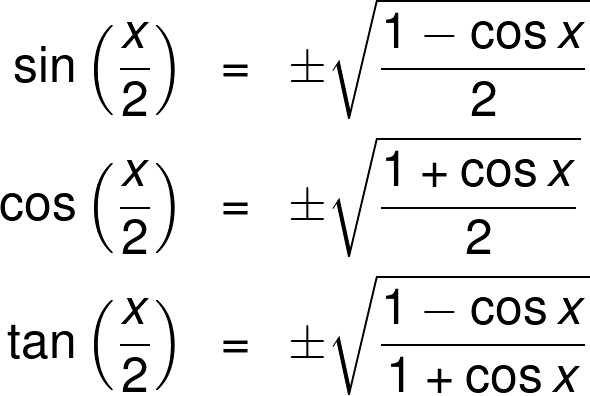
Half Angle Calculator

$$tan(2θ)={2 tan(θ)}/{1– tan^2(θ)}$$ Additional Trig Identities These three categories of trig identities are used less often You should look through them to make sure you understand them, but they typically don't need to be memorized HalfAngle Identities These are inversions of the doubleangle identities $$sin2(θ) = {1/2}(1cos (2θ))$$ · Match the trigonometric functions (such as tan) with those on the opposite side The rest of the side is known as the adjacent side, and is used to discover the cosine Or perhaps you transform both sides into the same expression For example, if you have two terms on the left side and only one term on the correct side, find the frequentTrigonometric Identities prove tan^2 (x)sin^2 (x)=tan^2 (x)sin^2 (x)

Trig Identities Bingo Card

Solved 2 Prove The Following Trig Identities A Prove Chegg Com

Trigonometric Identities The Six Trigonometric Functions Reciprocal Identities ℎ 1 sin = ℎ = csc = = cos = ℎ = sec = ℎ = tan = = cot = = 1 sin = csc csc = sin 1 tan 2 = 1cos sin Co Function Identities sin 0 $1,=cos csc 0 $1,=sec cos 0 $1,=sin secStuck on a trig identities question could someone please point me in the right direction 2tanθ / 1 tan^2θ = 1/2 (sorry about it not being in latex fSec, cosec and cot;

Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions

How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic

Mathematics Revision Guides – Further Trigonometric Identities and Equations Page 7 of 17 Author Mark Kudlowski Example (5) Use the result of the previous example to express cos 2A in terms of tan A Since A A A cos2 sin2 tan2 , it follows that A A A tan2 sin2 cos2 A A A tan 2 1 cos 2 sin 2 cos 2A A A A A 2tan 1 tan 1 tanTrigonometry Identities Examples and Strategies cosine is an "even" identity;We try to relate the given equation to one of our three identities We can use the identity sec2 x = 1tan2 x to rewrite the equation solely in terms of tanx 2tan2 x = sec2 x 2tan 2x = 1tan x from which tan2 x = 1 Taking the square root then gives tanx = 1 or − 1 The graph of tanx between 0 and 2π is shown in Figure 2 Note that the function values repeat

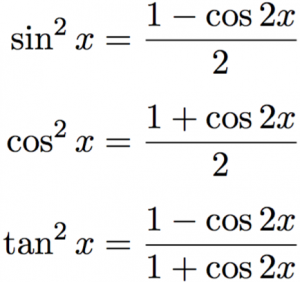
Trig Identities Table Of Trigonometric Identities

How I Remember Trig Identities Part 2 Beyond Solutions

Pythagorean Trigonometric Identities For any theta, sin 2 θ cos 2 θ = 1 sin 2 θ cos 2 θ = 1 1 cot 2 θ = csc 2 θ 1 cot 2 θ = csc 2 θ tan 2 θ 1 = sec 2 θ tan 2 θ 1 = sec 2 θ Note that this need not me memorized, connect these to the Pythogoras theoremTrigonometry Degrees and radians;Legend x and y are independent variables, ;

Summary Of Trigonometric Identities

Tangent Half Angle Formula Wikipedia

Products of Sines and/or Cosines;Verify that cos (x)·tan (x) csc (x)·cos 2 (x) = csc (x) using trigonometric identities · There are three basic trigonometric identities in class 10 which relate the trigonometric ratios mutually The three basic trigonometric identities learned in class 10 are Sin2A Cos2A = 1 Sec2A = 1 Tan2A

List Of Trigonometric Identities Wikipedia

Art Of Problem Solving

Trigonometric identities are equations that relate different trigonometric functions and are true for any value of the variable that is there in the domain Basically, an identity is an equation that holds true for all the values of the variable(s) present in it (sin θcosec θ) 2 (cos θsec θ) 2 =7tan 2 θcot 2

Summary Of Trigonometric Identities

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

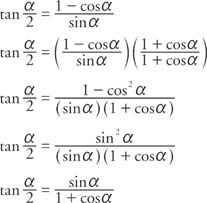
Tangent Identities

14 2 Trigonometric Identities

Ppt Analytic Trig Powerpoint Presentation Free Download Id

11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download

Fundamental Identities

Trigonometric Identity Examples Solutions Videos

Integrate Sec 2x Method 1

Tangent Half Angle Formula Wikipedia

5 1 Fundamental Trig Identities Reciprocal Identities Sin

Trigonometric Identity 1 Sin X 1 Sin X Sec X Tan X 2 Cbse 10 Youtube

Trig Identities Pdf Trigonometric Identities Fundamental Identities Sin 2 A Cos 2 A 1 1 Tan 2 A Sec 2 A 1 Cot 2 A Csc 2 A Sin A Sin A Cos A Cos A Tan Course Hero

What Is The Formula Of Tan2x Quora

Trig Identities All List Of Trigonometric Identities Learn Trigonometry

Trigonometric Integrals

Ilectureonline

14 2 Trigonometric Identities

While You Wait Trigonometric Identities And Equations Section

14 2 Trigonometric Identities

Cochranmath Solving Trigonometric Equations

3 1 Reciprocal And Pythagorean Identities Mathematics Libretexts

Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions

Trigonometric Identities A Plus Topper

Power Reducing Formulas And How To Use Them With Examples Owlcation

List Of Trigonometric Identities Wikipedia

How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic

How To Prove Quotient And Reciprocal Identities Studypug

Trig Integrals Trig Substitution

Chapter 5 Trigonometric Identities Review Sheet

7 4 Proving Trigonometric Identities In This Unit We Ll Be Using Some Formula S That Are Also Found And Used In Unit 7 2 And 7 3 Here We Ll Be Solving Problems To Show That Both Sides Of The Equation Equal Each Other These Formulas Will Help Solve Some Trig

Verifying Trigonometric Identities Process Make One Side Look

Solved We Wish To Prove The Following Trig Identity Tan Chegg Com

7 Proving Ids Trig Functions Identities

14 2 Trigonometric Identities

Trig Identities Table Of Trigonometric Identities

Trig Identities Bingo Card

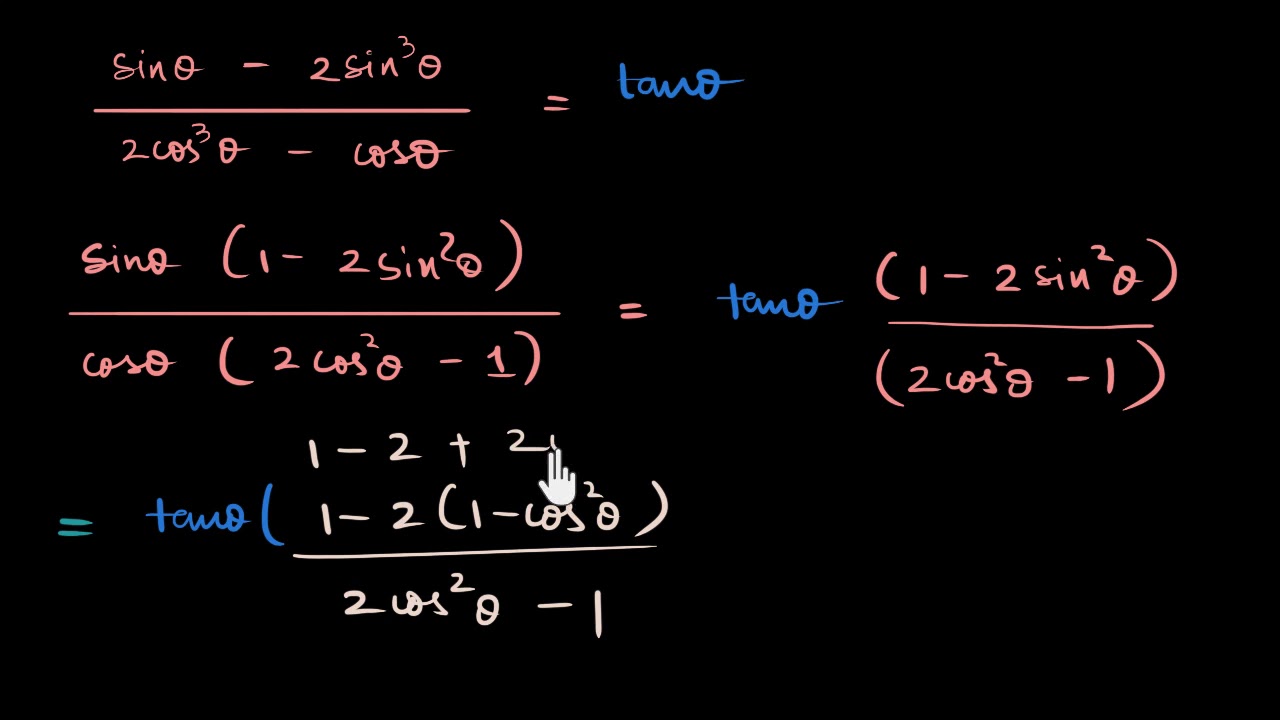
Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy

Trig Identities Worksheet With Answers 2

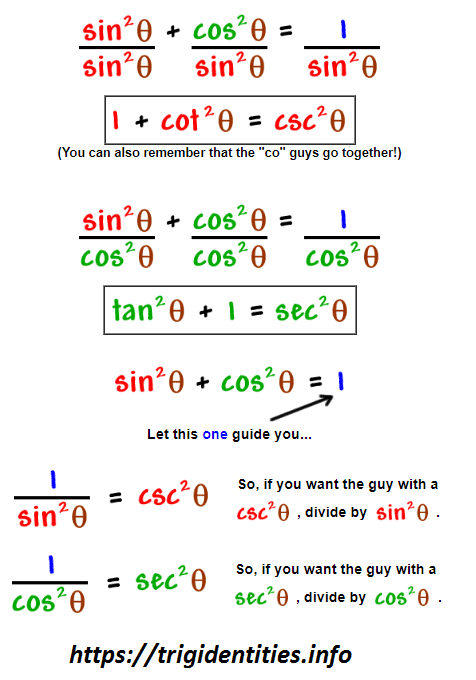
Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

Summary Of Trigonometric Identities

Trigonometric Identities A Plus Topper

What Does It Mean To Prove A Trigonometric Identity Socratic

Trigonometric Identities Topics In Trigonometry

Trigonometric Identities

Trigonometric Identities List Of Trigonometric Identities Examples

Solved We Wish To Prove The Following Trig Identity Cos Chegg Com

Powers Of Trigonometric Functions

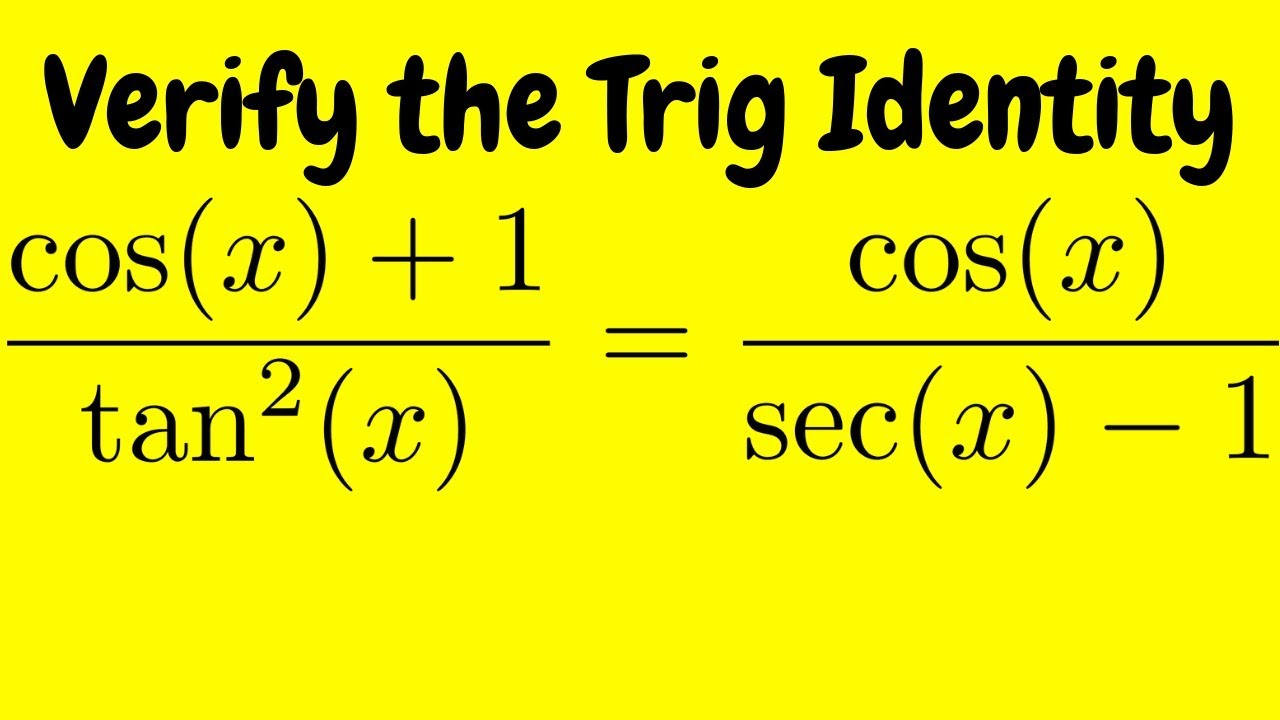
Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube

Lesson 5 2 Verifying Trigonometric Identities Trig Ridge Style

Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube

2sinxcosx Identity Gamers Smart

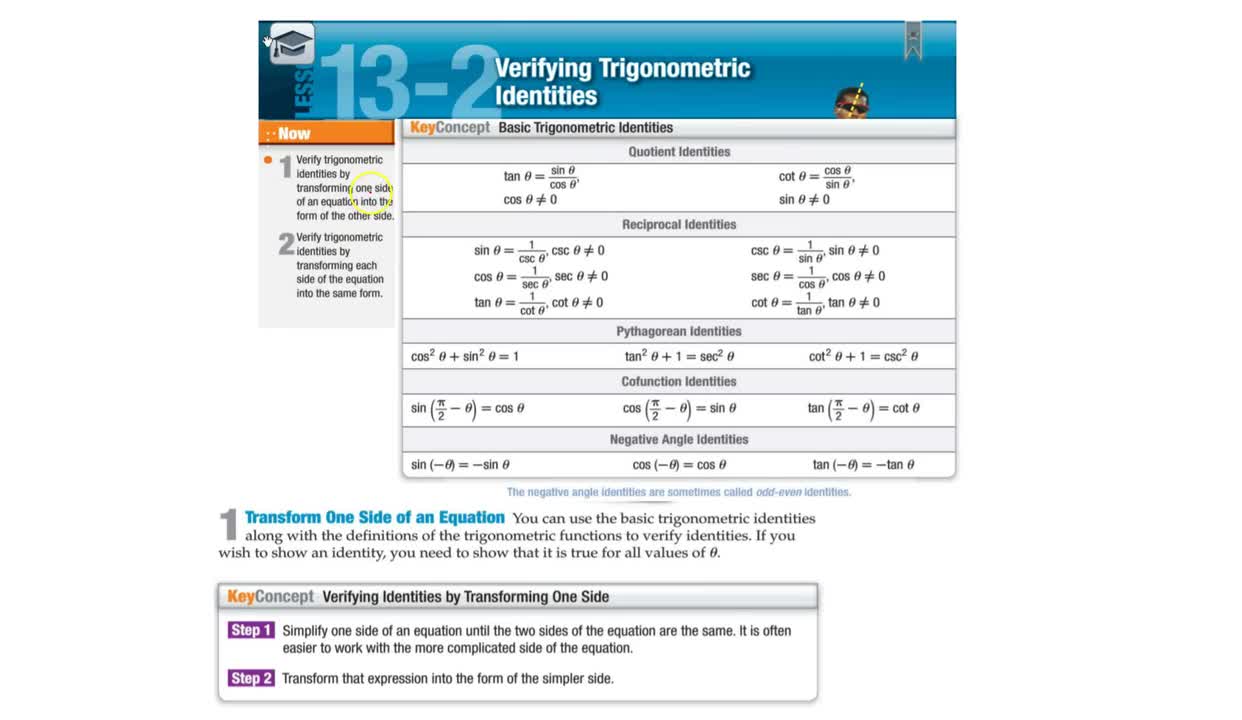
Honors Algebra 2 Trig Notes Chapter 13 Section 2 Bishop Amat Memorial High School

10 4 Integration Of Powers Of Trigonometric Functions

10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com

Tangent Identities

Tangent Identities

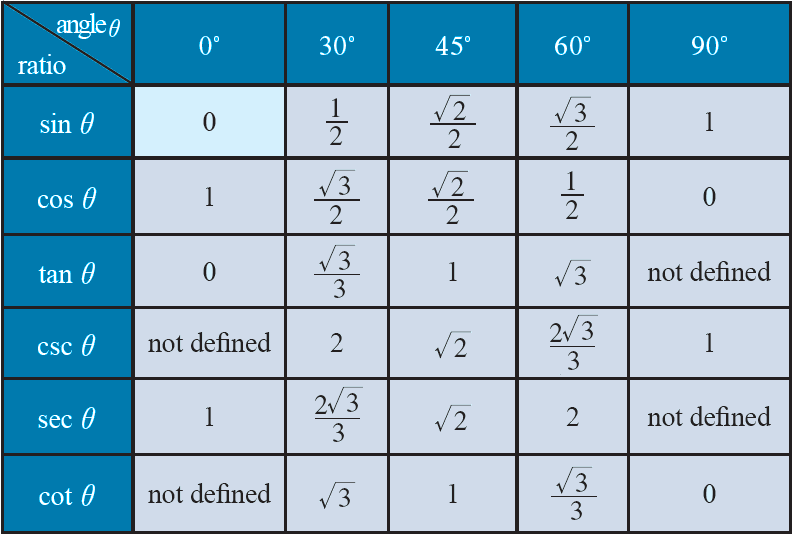
Trigonometric Identities

Sum And Difference Identities Video Lessons Examples And Solutions

Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube

6 1 2 Trigonometric Identities

Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

Solved Simplify Each Of The Following Trigonometric Expre Chegg Com

What Are The Quotient Identities For A Trigonometric Functions Socratic

The Trigonometric Ratios Of Angl

Trig Identities Study Sheet

Chapter 11 Trigonometric Identities And Equations 11 1

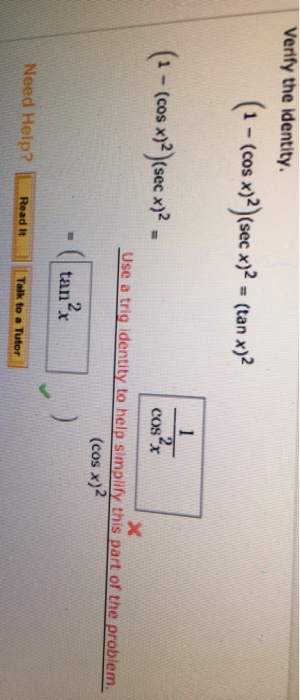
Solved Verify The Identity 1 Cos X 2 Sec X 2 Tan Chegg Com

Worksheet On Trigonometric Identities Establishing Identities Hints

Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube

Incoming Term: trig identities tan^2, trig identities tan^2 theta,