So,our formula becomes `x^3 y^3 z^3 3xyz =0**(x^2y^2z^2xyyzzx)` `x^3 y^3 z^3 3xyz =0` `x^3 y^3 z^3 = 3xyz ` ← Prev Question Next Question → Related questions 0 votes 1Solve for x Use the distributive property to multiply xy by x^ {2}xyy^ {2} and combine like terms Use the distributive property to multiply x y by x 2 − x y y 2 and combine like terms Subtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0 if x=3 and y=4 find the value of x(3x4y) If Doraemon had anywhere door, then why Nobita always got late for school xD Solve for the two x values using the quadratic formula method

Ex 2 5 14 Without Actually Calculating The Cubes Find I 12 3
X^3+y^3+z^3-3xyz formula proof
X^3+y^3+z^3-3xyz formula proof-How do you factor completely x^3 y^3 z^3 3xyz?I don't know what you really want to ask , but here is at least a bit of content to this for this formula Since it is homogenous in x,y,z (so all terms have equal degree), you can read it as a description of a object of algebraic geometry either
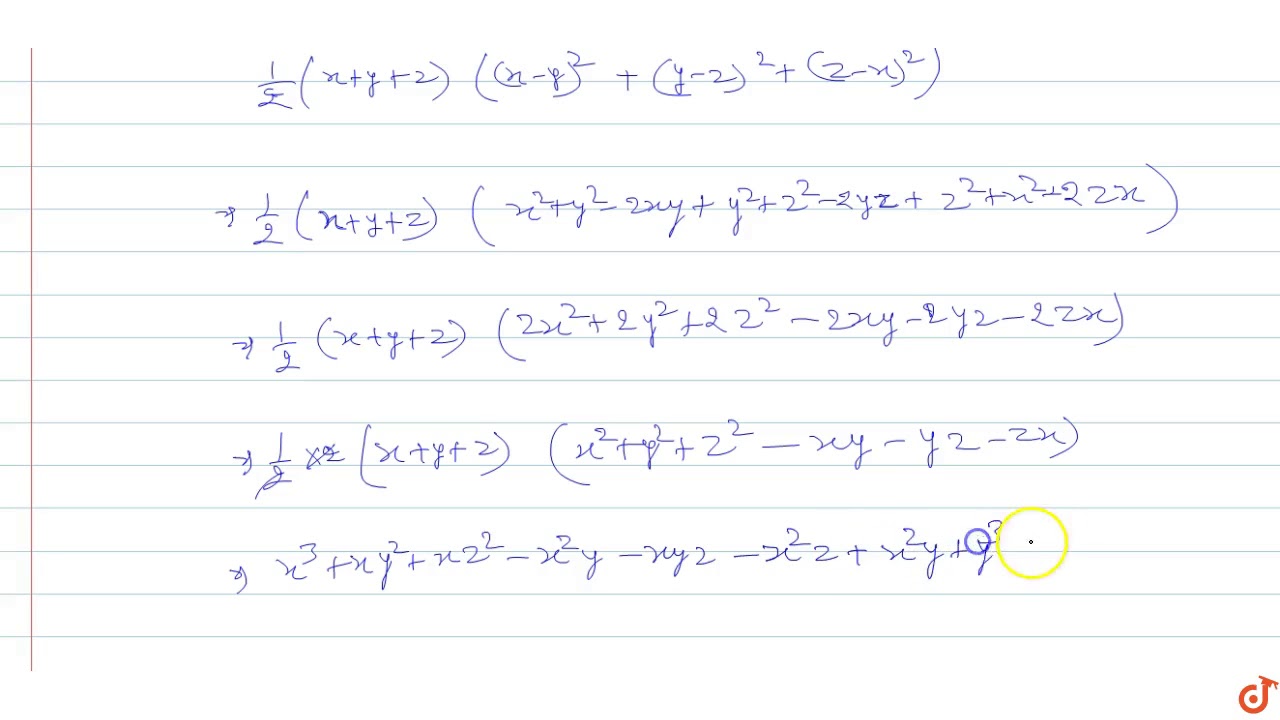



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube
In mathematics, the Poincaré residue is a generalization, to several complex variables and complex manifold theory, of the residue at a pole of complex function theoryIt is just one of a number of such possible extensions Given a hypersurface defined by a degree polynomial and a rational form on with a pole of order > on , then we can construct a cohomology class (;)Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations x3(yz)y3(zx)z3(xy) so that you understand betterSolution x = 2x, y = 2y and z = 4z If x y z = 0, then x 3 y 3 z 3 = 3xyz 8x 3 27y 3 64z 3 = 3 (2x) (2y) (4z) = 48xyz After having gone through the stuff given above, we hope that the students would have understood, "x cube plus y cube plus z cube minus 3xyz" Apart from the stuff given in this section, if you need any other
Ex 25, 12 Verify that x3 y3 z3 – 3xyz = 1/2 (x y z)(x – y)2 (y – z)2 (z – x)2 Solving RHS 1/2 (x y z)(x – y)2 (y – z)2 (z – x Given If x y = 4, xy = 2, y z = 5, yz = 3, z x = 6 and zx = 4 Formula used x 3 y 3 z 3 3xyz = (x y z) × (x 2 y 2 z 2 – xy – yz – zx) (x y) 2 = x 2 y 2 2xy Calculations x y = 4, y z = 5, z x = 6 So, x y z = 15/2 = 75Get the answer to this question and access a vast question bank that is tailored for students
L #shorts l Algebra Identities l algebra l Algebra formula l math lHow to solve If xy=z Then x^3y^3z^33xyz=?L #short l #shortvideo l #careermadeeasy l math shorts lX^3 y^3 z^3 3x^2y 3xy^2 3x^2z 3z^2x 3y^2z 3z^2y 6xyz Lennox Obuong Algebra Student Email obuong3@aolcom




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube
A) 36 b) 40 c) 42 d) 48बीजगणित सामान्य सूत्र (Math Algebra Basic Formula) Magic Maths Tricks In Hindi16 SSC IBPS बीजगणित सामान्य सूत्र (Math Algebra Basic Formula) X 3 Y 3 Z 3 =3XYZIf x y z = 6 and xy yz zx = 10, then the value of x3 y3 z3 3xyz is?



If X Y Z 6 And X2 Y2 Z2 Then The Value Of X3 Y3 Z3 3xyz Is From Quantitative Aptitude Algebra



X 3 Y 3 Z 3 3xyz Formula Proof Malaydras
If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____ formula of polynomials Questions;X = 551, y = 552 and z = 557 we know the alternate way to write the for대수 인수분해하기 x^3y^3z^3 x3y3 z3 x 3 y 3 z 3 x3y3 x 3 y 3 을 (xy)3 ( x y) 3 로 바꿔 씁니다 (xy)3 z3 ( x y) 3 z 3 두 항 모두 완전세제곱식이므로 세제곱의 합 공식 a3 b3 = (ab)(a2 −abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) 을 이용하여 인수분해합니다 이 때 a = xy a = x y




Dziedzictwo Lekarstwo Mary X 3 Y 3 Wierzcholek Pochylac Sie Usunac



What Is The Formula Of Math X 3 Y 3 Z 3 3xyz Math Quora
If there doesnt exist real solution, then the cubic equation has 3 roots and it's easy to use trigonometry to solve it (applying the formula $\cos 3x =4\cos^3 x 3 \cos x$) But this is not the case that we are interested in{eq}x^3 2y^3 z^3 3xyz 2y 3 = 0 {/eq} Implicit Differentiation Let us use the implicit differentiation to find the partial derivative that is we will keep only the x as variable while yFind the zeros of the polynomial 4x square 25;




If X Y Z 0 Show That X3 Y3 Z3 3xyz Maths Polynomials Meritnation Com
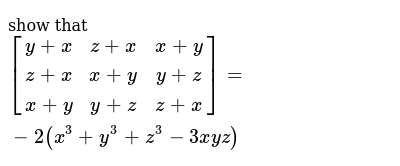



Show That Y X Z X X Y Z X X Y Y Z X Y Y Z Z X 2 X 3 Y 3 Z 3 3xyz
If xy=z Then x^3y^3z^33xyz=? Find an answer to your question verify that x^3 y^3 z^3 3xyz = 1/2(x y z)(x y)^2 (y z)^2 (z x)^2 Answer First We take RHS & use the Formula ( ab)²= a²b²2ab & simplify it then RHS becomes equal to LHSSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




X 3 Y 3 Z 3 Novocom Top




4 Partial Derivatives And Their Applications Derivative Variable Mathematics
#shorts l Algebra Identities l algebra l Algebra formula l math l How to solve If xy=z Then x^3y^3z^33xyz=?Factoring Calculator Online calculator factors single variable or multivariable polynomial with step by step explanations Start by entering your expression in the formula pane below Example x 4 x 2 1, x 6 64 y 6, x 3 y 3 z 3 − 3 x y z Solve Factoring Calculator Equation SolverClick here👆to get an answer to your question ️ Using the identity and proof x^3 y^3 z^3 3xyz = (x y z)(x^2 y^2 z^2 xy yz zx) Join / Login maths



X Y Z 3 Expansion




Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 And Then Factorize 64x3 125y3 64z3 240xyz Brainly In
10 A polynomial from Qx, y, z is a polynomial from Qx, yz, so it can be viewed as a polynomial in z with coefficients from the integral domain Qx, y p(z) = z3 − 3xy ⋅ z x3 y3 So we can try our methods to factor a polynomial of degree 3 over an integral domain If it can be factored then there is a factor of degree 1, we call= x 3 y 3 z 3 – 3xyz (all the other terms are canceled) Hence the formula is derived Factoring Formula 9 x 3 y 3 = (x y) (x 2 – xy y 2) Let us start with the righthand side of this formula and reach the lefthand side at the end (x y) (x 2 – xy y 2) = x 3 x 2 y xy 2 x 2 y xy 2 y 3 = x 3 y 3 Hence the formulaCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




Formula




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer
Solution for Find the value of x3 y3 z3 3xyz if x2 y2 z2 = x y z = 15Or, `x^3 y^3 z^3 3xyz = 0` Or, `x^3 y^3 z^3 = 3xyz` proved Question 14 Without actually calculating the cubes, find the value of each of the followingQuestion If x = 255, y = 256, z = 257, then find the value of x 3 y 3 z 3 3xyz Options




If X Y Z 0 Show That X 3 Y 3 Z 3 3x Y Z




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Class 9th Ex 2 5 Question 12 Youtube
Answer The formula of x 3 y 3 z 3 – 3xyz is written as Let us prove the equation by putting the values of x = 1 y = 2 z = 3 Let us consider LHS of the equation LHS = x 3 y 3 z 3 – 3xyz LHS = 1 3 2 3 3 3 – 3 (1 × 2 × 3) Ex 25, 13 If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence pro The answer is yes, the rational points on your surface lie dense in the real topology Let's consider the projective surface S over Q given by X 3 Y 3 Z 3 − 3 X Y Z − W 3 = 0 It contains your surface as an open subset, so to answer your question we might as well show that S ( Q) is dense in S ( R) Observe that S has a singular



If X A Y B Z C Show That X 3 A 3 Y 3 B 3 Z 3 C 3 3xyz Abc Sarthaks Econnect Largest Online Education Community




If X Y Z 0 Then Show That X3 Y3 Z3 3xyz If X Y Z 0 Prove That X3 Y3 Z3 3xyz Youtube
Click here👆to get an answer to your question ️ Factorise 27x^3 y^3 z^3 9xyz Formula of a plus b whole cube (a plus b whole cube formula) Dear Examtrixcom (Exam Tricks) followers, That is to say, this important PDF Book is about ab whole cube formula Similarly, at this platform we share a plus b ka whole cube Handwritten notes pdf in HindiEnglish and ab cube formula Free Pdf Study material for Sarkari exam Jobs(xyz)^3 put xy = a (az)^3= a^3 z^3 3az ( az) = (xy)^3 z^3 3 a^2 z 3a z^2 = x^3y^3 z^3 3 x^2 y 3 x y^2 3(xy)^2 z 3(xy) z^2 =x^3 y^3 z^3 3 x




X3 Y3 Z3 Novocom Top




X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Novocom Top
Example 1 Simplify (3u 5w) (3u – 5w) Using the algebraic identities (a b) (a b) = a2 b2, we substitute a for 3u and b for 5w (3u 5w) (3u – 5w) = (3u)2 – (5w)2 = 9u2 – 25w2 Thus (3u 5w) (3u – 5w) = 9u 2 – 25w 2 Example 2 Using the algebraic identities to simplify (3a 7b)2 Using (ab)2 = a22abb2Learn about Algebra Formula, Equations and List of Basic Algebraic Formulas & Expression in Math Algebra includes real numbers, complex numbers, matrices, vectors and many other topics(xyz) (x ^ 2 xy y ^ 2 xzyz z ^ 2) หลักฐาน โปรดทราบว่า x = y z เป็นคำตอบของ x ^ 3y ^ 3z ^ 33xyz = 0 เสียบ x = y z ในสมการข้างต้น (y z) ^ 3y ^ 3z ^ 33 (y z) yz = y ^ 3 3y ^ 2z 3yz ^ 2 z ^ 3 y ^ 3z ^ 33y ^ 2z3yz ^ 2 = 0 เราจึงสามารถหาร




Algebra Toughest Questions Algebra Teaching Mathematics




Factorise The Following X Y 2 X Y 2 Factorise X Y 2 X Y 2
We believe that the comprehensive list of basic Maths formulas for Class 9 will make your learning effective You can simply click on the Topics to view the Class 9 Maths formulas and aid your preparation If you feel any formula is missing that can be added to our list do drop us a comment and we will add it to the list Answer is (xy z)(x^2 y^2 xyz z^2) You can check by multiplying it out Notice that each term is a perfect cube x^3 y^3 = (xy)^3 So we have a sum of cubes, and the factoring formula is a^3 b^3 = (ab)(a^2abb^2) So we use a = xy and b = z to get x^3 y^3 z^3 = (xy)^3 z^3 = ((xy) z)((xy)^2(xy)zz^2) =(xy z)(x^2 y^2 xyz z^2) check by multiplying it out toIf x = 551, y = 552 and z = 557, then what is the value of x 3 y 3 z 3 – 3xyz?




Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2




Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z
गुणनखंड कीजिये `x^(3) y^(3) z^(3) 3xyz`Solution (By Examveda Team) Given, x y z = 0 Cubing both side, (x y z) 3 = 0 x 3 y 3 z 3 3xyz = 0 using formula x 3 y 3 z 3 = 3xyz 3 Follow 1 Certified by MeritNation Expert Yogendra Singh, added an answer, on 10/9/12 Yogendra Singh answered this Given xyz=0 to prove x 3 y 3 z 3 =3xyz x 3 y 3 z 3 3xyz= (xyz)



If X A Y B Z C Show That X 3 A 3 Y 3 B 3 Z 3 C 3 3xyz Abc Sarthaks Econnect Largest Online Education Community
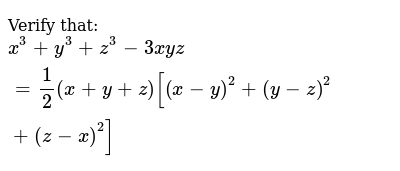



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z
The diophantine equation x^3/3y^3z^32xyz=0 We will be presenting two theorems in this paper The first theorem, which is a new result, is about the nonexistence of integer solutions of the cubic diophantine equation In the proof of this theorem we have used some known results from theory of binary cubic forms and the method of infiniteAnswer to For f(x,y,z) = x^3y^3z^33xyz, evaluate the directional derivative f prime (1,1,1(a,b,c)) at the point (1,1,1) towards the directionTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Verify that `x^3y^3z^33x y z=1/2(xyz)(xy)^2(yz)^2(zx)^2`




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer




If X Y Z 9 And X 2 Y 2 Z 2 35 Find The Value Of X 3 Y 3 Z 3 3xyz Brainly In



1




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In




Polynomials Ppt Video Online Download




Bits Of Math Problem Cubes And Cube Roots




If X Y Z 0 Show That X3 Y3 Z3 3xyz Maths Polynomials Meritnation Com
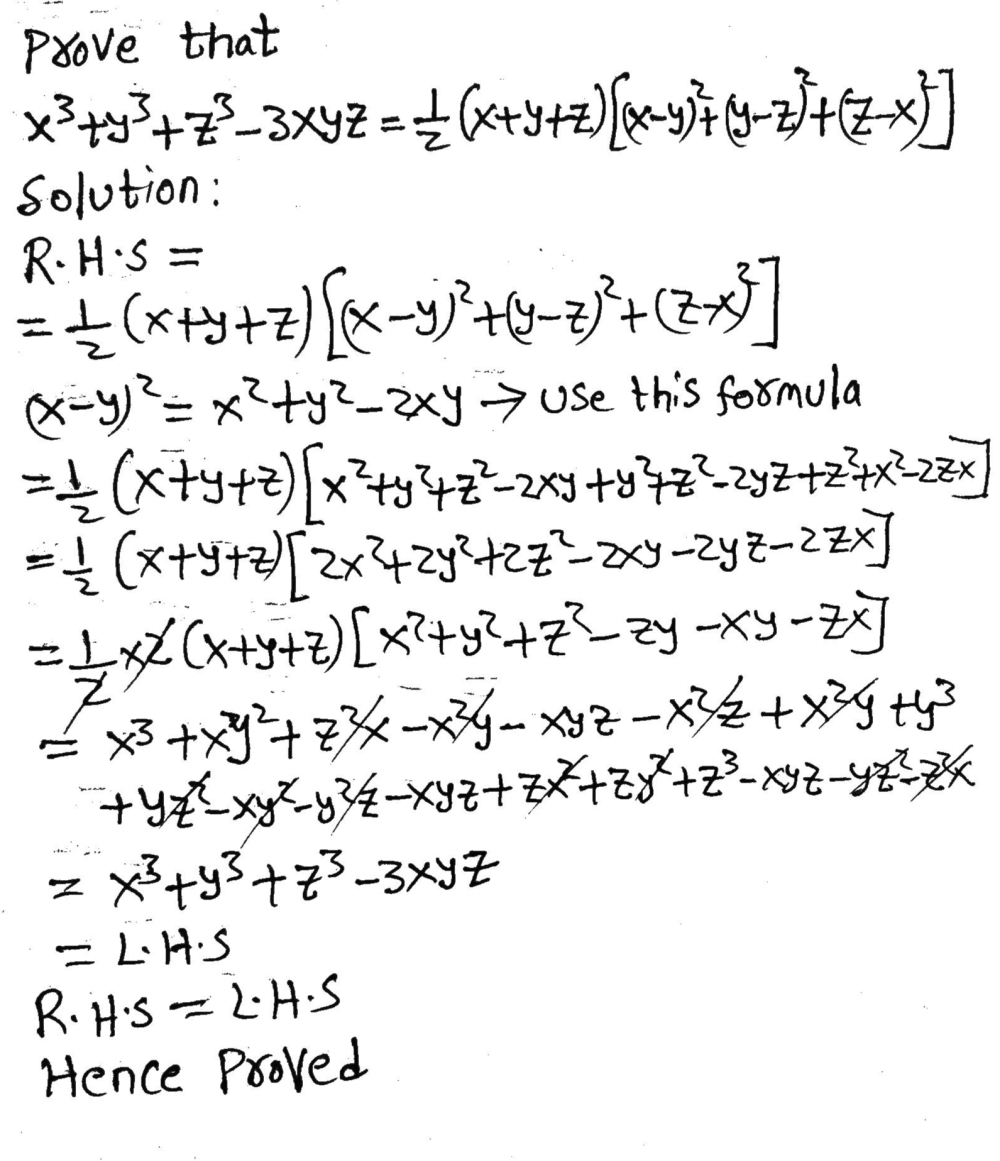



Verify That X 3 Y 3 Z 3 3xyz Frac 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Snapsolve



If X Z 225 And Y 226 Then What Is The Value Of X Y Z 3xyz Quora




X 3 Y 3 Z 3 3xyz の因数分解についての話題から 身勝手な主張




If Math X Y Z 0 Math Then Math X Y Z 3 Y Z X 3 Z X Y 3 Math Quora




2
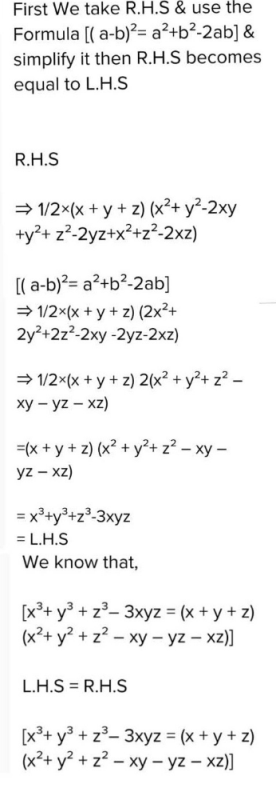



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Can Any One Solve This Question Edurev Class 9 Question



Cbse 9 Math Cbse Polynomials Ncert Solutions




Prove That 1 1 1 X Y Z X 3 Y 3 Z 3 X Y Y Z X Y Z




Prove That X3 Y3 Z3 3xy X Y Z X2 Y2 Z2 Xy Yz Zx Only By Lhs Brainly In




Polynomials Ppt Video Online Download




What Is The Formula For A 3 B 3



1




Pdf On Some Properties Of Xi Yi Zi Dxyz X3 Y3 Z3 Dxyz And X6 Y6 Z6 Dxyz And A Critique Of Solutions For The Markoff Equation X2 Y2 Z2 Axyz




X Y Z 0 Show That X3 Y3 Z3 3xyz Novocom Top



Using Identities Prove That X 3 Y 3 Z 3 Or Equal To 3xyz Where X Y Z Are Positive Real Numbers Quora




Ex 2 5 14 Without Actually Calculating The Cubes Find I 12 3




If X A B Y B C Z C A Then X3 Y3 Z3 3xyz Brainly In



Arxiv Org Pdf 1609
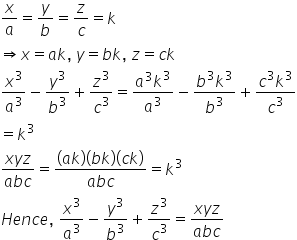



If X A Y B Z C Then Show That X3 A3 Y3 Z3 A Xyz Abc Mathematics Topperlearning Com Mfmw0q55




If X Y Z 0 Show That X3 Y3 Z3 3 Xyz Brainly In




Ex 2 5 14 Without Actually Calculating The Cubes Find I 12 3



If Math X Y Z 0 Math How Do You Prove That Math X 3 Y 3 Z 3 3xyz Math Quora




X Y Z 0 Show That X3 Y3 Z3 3xyz Novocom Top




Polynomials Ppt Video Online Download



Www Vidyarthiplus Com Vp Attachment Php Aid 7157




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube



If X Z 225 And Y 226 Then What Is The Value Of X Y Z 3xyz Quora




X3 Y3 Z3 Novocom Top



Http People Whitman Edu Hundledr Courses M225 Rev2soln Pdf




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz Brainly In




Ex 2 5 11 Factorise 27 X3 Y3 Z3 9xyz Class 9 Ex 2 5
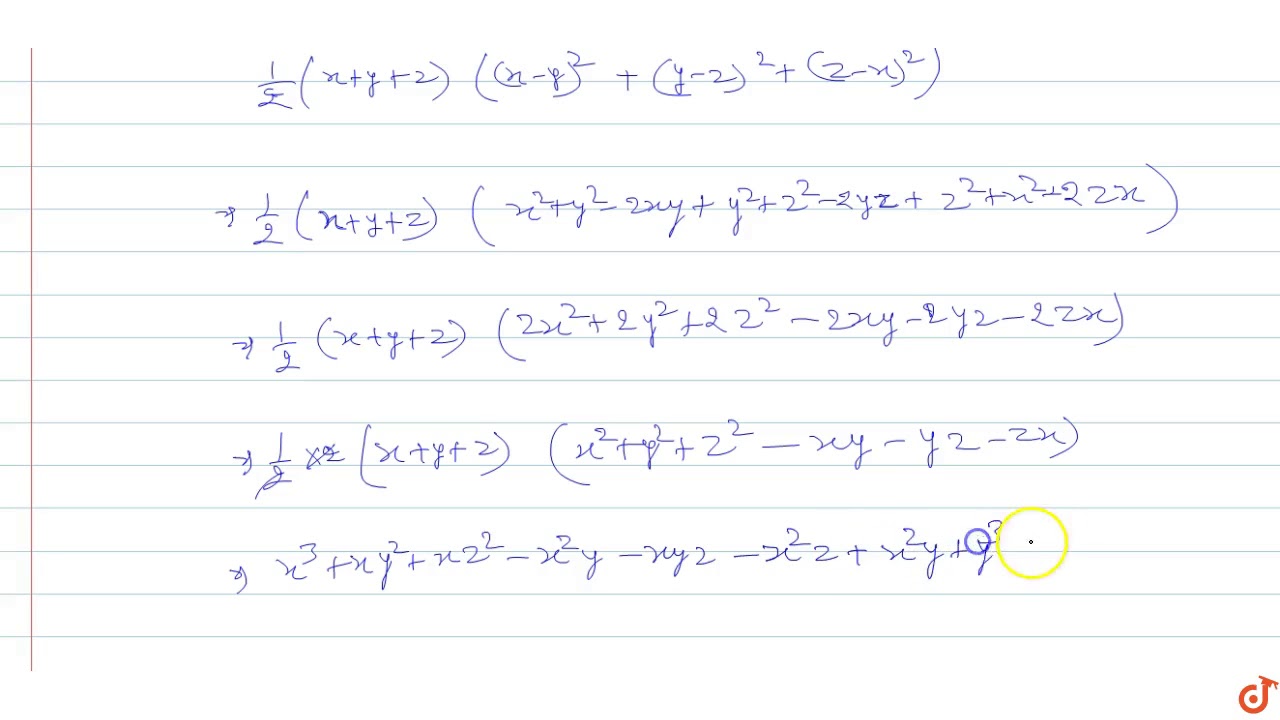



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Verify That 3 3 3 3 12 2 2
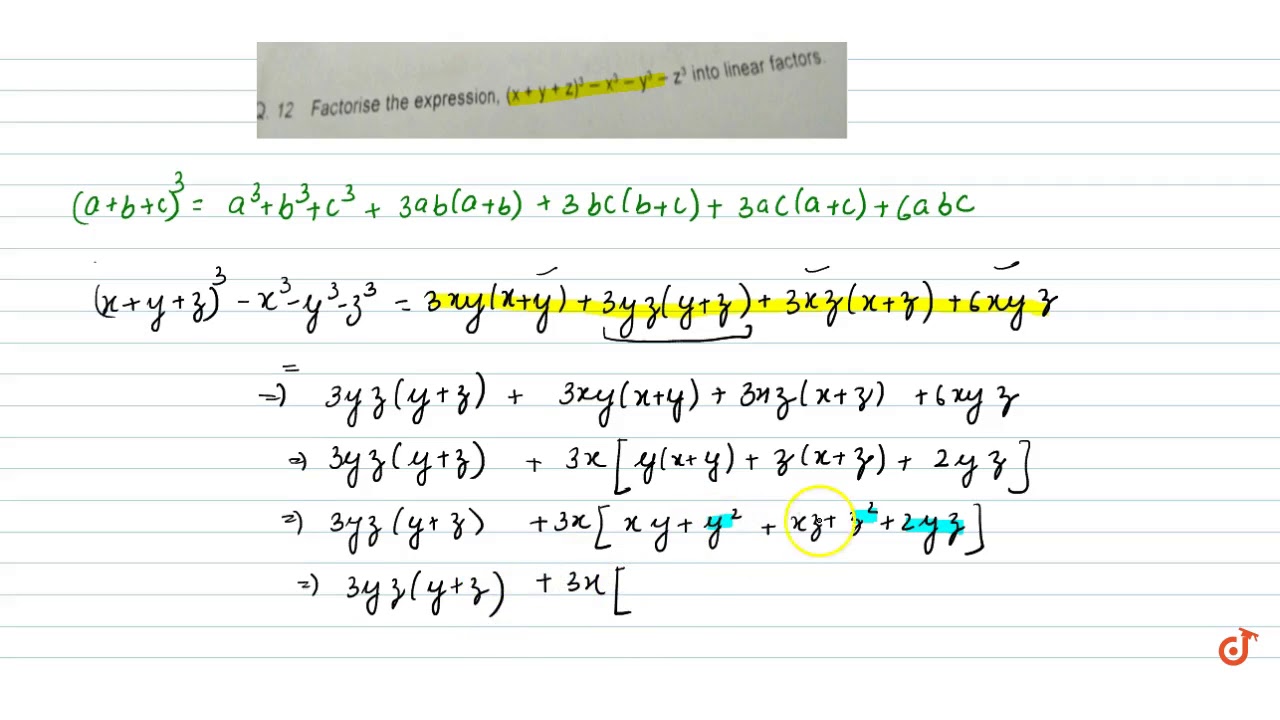



Q 12 Factorise The Expression X Y Z 3 X3 Y3 Z3 Into Linear Factors Youtube



If X Y Z 9 And Xy Yz Zx 23 Find The Valure Of X3 Y3 Z3 3xyz Brainly In




Prove That X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Maths Meritnation Com




Rd Sharma Class 9 Chapter 5 Factorization Of Algebraic Expressions




Factorization Of X3 Y3 Z3 3xyz Youtube




If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz Youtube




Prove That X Y3 Y Z3 Z X3 3x Yy Zz X 2x3 Y3 Z3 3xyz Maths Polynomials Meritnation Com




Prove That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In



Http Www Cis Umac Mo Fstitl Calculus12 13 Example 04 Pdf
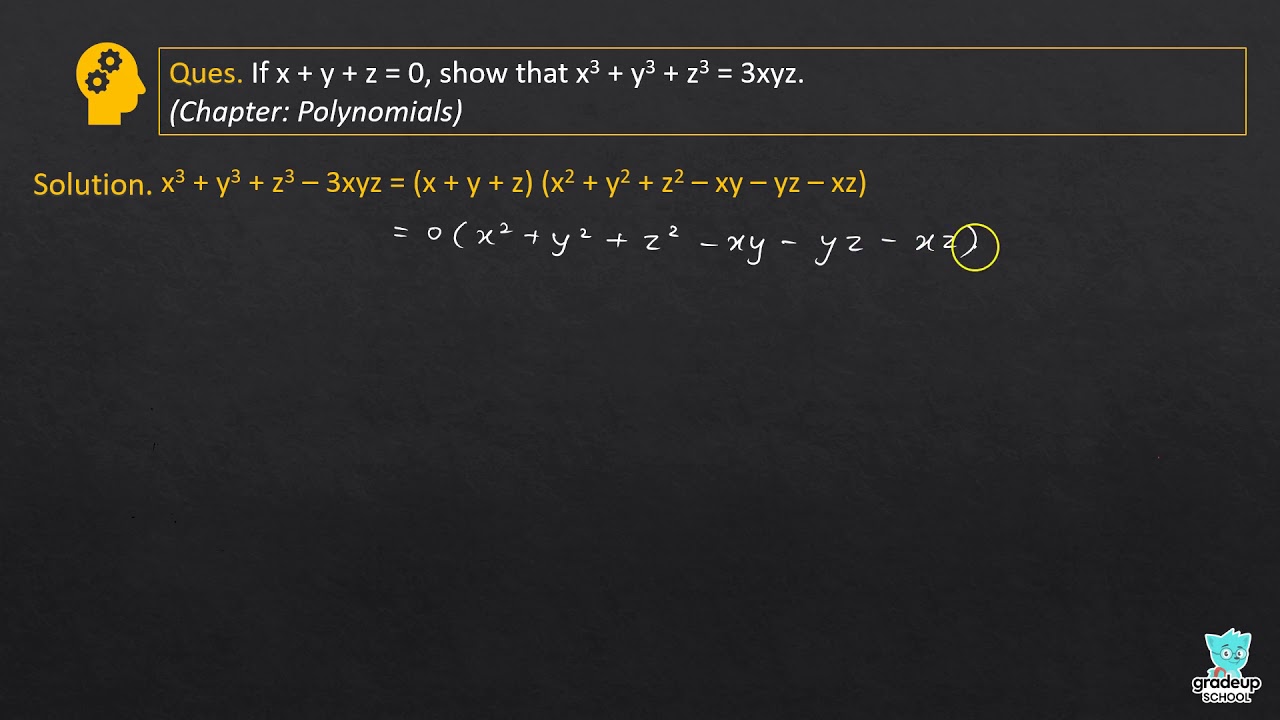



Ex 2 5 Q13 If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz




If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz




X Y Z 0 Show That X3 Y3 Z3 3xyz Novocom Top




If X 3 Y 3 Z 3 3xyz Then X Y Z




X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Novocom Top




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video




File



Search Q X Y 5e3 Tbm Isch




Polynomials Ppt Video Online Download



What Is The Formula Of Math X 3 Y 3 Z 3 3xyz Math Quora



What Is The Smallest Value Of X 2 Y 2 Z 2 Assuming X Y Z Are Real Numbers Satisfying X 3 Y 3 Z 3 3xyz 1 Quora




Polynomials Ppt Video Online Download




2




Show That X3 Y3 Z3 3xyz X Y Z X2 Y2 Chegg Com




I Need An Example For This Formula X3 Y3 Z3 3xyz Brainly In




If X Y Z 0 Then Show That X3 Y3 Z3 3xyz




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer




X Y Z 0 Show That X3 Y3 Z3 3xyz Novocom Top




If Math X Y Z 0 Math What Is The Value Of Math Frac X 2 Yz Frac Y 2 Zx Frac Z 2 Xy Math Quora




X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In




Exercise




Find The Value Of X 3 Y 3 Z 3 3xyz If X 2 Y 2 Z 2 And X Y Z 15 Brainly In




2 Two Cube 5 Five Cube 10 Ten Cube Pdf Free Download



What Will Be The Value Of X Y Z 3 If X Y Z 0 Quora




Polynomials Pages 1 28 Flip Pdf Download Fliphtml5



0 件のコメント:
コメントを投稿